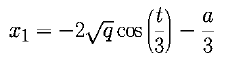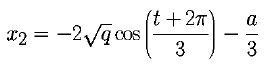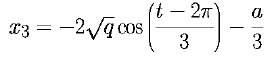(This is a hard dead-line for both hard copy and drop-box submission. Do not leave it to the last minute. `I couldn't get my printer to work' or `The network was down at 4:30' are not accepted excuses for lateness.)
Don't forget to include the specified header comment.
Question 1
The sequence of Fibonacci numbers begins with the integers1, 1, 2, 3, 5, 8, 13, 21, ...where each number after the first two is the sum of the two preceding numbers. In this sequence, the ratios of consecutive Fibonacci numbers (1/1, 1/2, 2/3, 3/5, ...) approach the "golden ratio"
sqrt(5) - 1
-----------
2
Write a program to calculate all the Fibonacci numbers smaller than 5000 and the decimal values of the ratios of consecutive Fibonacci numbers.
Your program should report how many Fibonacci numbers are generated and, for every 5'th number, the values of the ratio of (the 4'th to the 5'th) Fibonacci numbers and the difference from the Golden Ratio.
File name: fib-rat.cpp
Question 2
It is assumed that all first year students are familiar with the quadratic equation and how to solve for the roots of quadratic functions.
A less known technique is available for calculating the roots of cubic equations of the form x3 + ax2 + bx + c = 0. To solve such an equation you first compute the two values:
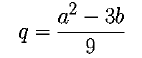
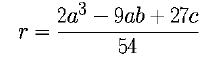
***
If r2 is less than or equal to
q3 then there are three solutions. To compute
these solutions you first calculate
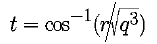
then use this value to find the solutions:
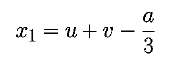
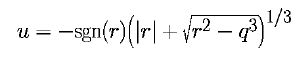
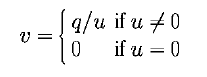
The sgn(x) is a function that returns 1 if x >= 0 and returns -1 otherwise.
***
Test your program on the cubics:
x3 - x2 + 2x -2
and
x3 - 6x2 + 11x -6
Report your results for these on the printed version of your solution.
OPTIONAL:
Test your program on the cubic:
x3 - 5x2 + 8x -4
Factor this cubic (hint: 1 is a root!) Can you explain your results?
File-name: cubic.cpp