|
|
|||
| 11. Invariance relations and set symmetry. |
When sets are transposed (Tn) or inverted and transposed (TnI), their pc content may
- Completely change. Transposing set [3,5,6,9] up by 5 semitones
(T5) yields set [8,10,11,2]. This new set shares none of
its pcs with [3,5,6,9]; it is wholly variant from [3,5,6,9].
Likewise T1I of [3,5,6,9] yields set [4,7,8,10], also completely
variant from the original set.
- Partly change. T3 of [3,5,6,9]
yields set [6,8,9,0],
preserving pcs 6 and 9. T10I of [3,5,6,9]
yields set [1,4,5,7], this time preserving
just pc 5. Both of these new sets are partly invariant from the
original set (though they vary completely from each other).
- Remain completely the same. Both T0 (of course) and T6 of set [2,3,8,9] yield [2,3,8,9] again. And both T5I and T11I of [2,3,8,9] return those same four pcs. Set [2,3,8,9] happens to remain wholly invariant under these four operations.
Composers often appear to make use of variance and invariance properties among sets of the same class. For instance, partial pc invariance among sets can be a marker that certain pcs (the invariant ones) are being stressed or made salient or that these pcs are acting as links among different sets. Conversely, a composer can avoid unwanted stress on pcs by making sure that pc content changes among different sets.
(You've long ago experienced the concrete effects of controlled pc invariance. Sets of class 7-35 (013568T)--the diatonic scale class--preserve 6 of their 7 pcs under T5 and T7, that is, when transposed by a perfect 4th or perfect 5th. That's why in tonal music the subdominant and dominant keys are so closely related to the tonic key.)
Symmetry
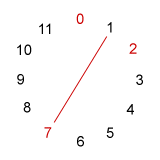
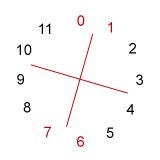
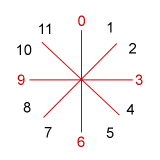
Complete invariance among sets is a marker of a set class's inherent symmetry: the more aspects of symmetry a set's intervallic arrangement possesses, the more times it will display complete invariance when transposed or inverted. We can illustrate this fact by looking at some sets on the 12-pc clockface. In Example 9-1 are displayed (in red) sets representing classes 3-9 (027) and two tetrachords, 4-9 (0167) and 4-28 (0369).
Example 9-1.
a. set 3-9 [0,2,7] b. set 4-9 [0,1,6,7]) c. set 4-28 [0,3,6,9]
- Notice the interval pattern of trichord [0,2,7] as we travel fully
around the clockface. If we begin and end at pc 7, we can arrange this
pattern symmetrically: 5 - 2 - 5. Now, this pattern does
not allow set [0,2,7] to be transposed (rotated about the clock) and
still comprise pcs 0, 2, and 7. So it's only invariant under the static
case of transposition T0. The red line, however, reveals
that this set does has an axis of inversional symmetry; notice
that the line splits the clockface into two mirror images. The set can
be inverted ("flipped") about this axis and retain the same pcs. Sure
enough, T2I of [0,2,7] is [0,2,7]. Since any set in class
3-9 will be invariant with an inverted version of itself, there are
only twelve, instead of twenty-four, distinct sets in this class.
- Sets of class 4-9 show more symmetry. First of all, its repeated interval
pattern around the clockface, 1 - 5 - 1 - 5, means that
it can be transposed invariantly. We can see that if set [0,1,6,7] is
rotated half-way around the clockface (that is, operation T6),
it will remain invariant. Furthermore, its two axes of inversional symmetry
indicate that at two inverted levels, (T1I and T7I),
the set will again be [0,1,6,7]. With four invariant versions of this
pretty symmetrical set, there are but six, rather than twenty-four,
distinct sets in class 4-9 (0167).
- Tetrachord 4-28 (familiar as the diminished-seventh chord) is more symmetrical still. It has an extremely regular interval pattern around the clockface: 3 - 3 - 3 - 3. Four different rotations of [0,3,6,9]--T0, T3, T6, and T9--will return the same pcs. And the four inversional-axis lines tell us that four inverted forms--T0I, T3I, T6I, and T9I--are also invariant. So we have eight invariant versions and only three distinct sets in class 4-28, a fact that you probably already knew about the diminished-seventh chord.
It is clear that, as they grappled with composing outside of the systematic underpinnings of tonality, many early 20th-century composers gravitated towards symmetrical properties (and not just in pitch structure) to give coherence to their compositions. Hence the popularity with these composers of such highly symmetrical set classes as the whole-tone scale, class 6-35 (02468T), and the octatonic scale, class 8-28 (0134679T).
Determining invariance
You may need at times to find out just how many pcs in a set will remain invariant under different levels of transposition or inversion. Here are some math shortcuts to help you. These shortcuts are based on the intervallic relations within and among sets. To save space, we'll just learn the shortcuts; later you can try figuring out their rationale (it's a great cure for insomnia).
Invariance under Tn
This one is simple: just use a set's interval-class vector, available in the table of pc set-classes. The number of pcs that will remain invariant when a set is transposed by n semitones is the same as the entry for n's interval class in the vector, except for ic 6, where it is double the entry. For example, let's try set [3,5,6,9] a set of class 4-12 (0236). The table tells us that the ic vector for this class is 112101.- Notice that this set contains just one interval of ic 1. If, then,
you transpose [3.5.6.9] by either T1 or T11, just
one pc should remain invariant. Well, T1 of [3,5,6,9]
is [4,6,7,10]. T11 of [3,5,6,9]
is [2,4,5,8].
- The ic vector contains no entries for ic 5. T5 of [3,5,6,9]
is the wholly variant [8,10,11,2]. T7 of [3,5,6,9] is [10,0,1,4].
- The ic vector entury again contains just one entry for ic 6. T6 of [3,5,6,9] is [9,11,0,3] as pcs 3 and 9 map onto each other.
Invariance under TnI
It's possible to construct vectors that can tell us about invariance under TnI levels, but they are a bother to use. Much easier is to construct an invariance matrix for the set you're examining. Below is such a matrix for set [3,5,6,9].
As in the example, we construct a matrix by
3 5 6 9 3 6 8 9 0 5 8 10 11 2 6 9 11 0 3 9 0 2 3 6
- writing out the set along the top and along the left side.
- adding all the pairs of numbers (in mod 12) to fill in the matrix.
In our matrix, for example, number 10 appears just once in the matrix, as the sum of 5+5. T10I of [3,5,6,9] is set [1,4,5,7], retaining just pc 5. However, number 11 appears twice in the matrix, as the sum of 5+6 and of 6+5. T11I of [3,5,6,9] is [2,5,6,8], mapping pcs 5 and 6 onto each other.
3 5 6 9 3 5 6 9 3 6 8 9 0 3 6 8 9 0 5 8 10 11 2 5 8 10 11 2 6 9 11 0 3 6 9 11 0 3 9 0 2 3 6 9 0 2 3 6
Even constructing matrixes is a bit tedious, of course, so you can let the computer do it for you. Jay Tomlin's set calculator, listed on the Other Sources page of this guide, will construct invariance matrixes for inversion as well as for transposition.
| Exercise 11-1. Invariance under Tn |
| Exercise 11-2. Invariance under TnI |
| Exercise 11-3. Set symmetry |
|
Key concepts on this page:
|
| Page last modified 10 July 2001 / GRT |
|
|||