|
|
|||
| 14. Complement relations. |
The overall pc universe in which sets operate is the chromatic scale, the aggregate of twelve pcs. The complement of a set comprises whichever pcs in the aggregate that set excludes. The set complement of tetrachord 4-12 [3,5,6,9], for example, is octachord 8-12 [7,8,10,11,0,1,2,4]; together, these two sets make up the aggregate.
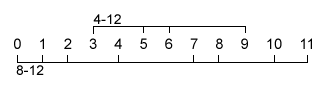
More abstractly, class 4-12 and class 8-12 are said to be complementary classes, because these classes include the above two complementary sets. If we take different sets in these same classes--for instance, 4-12 [0,3,4,6] and 8-12, [9,10,0,1,2,3,4,6]--such sets are considered to be "class complements" or "non-literal" complements. They no longer combine to make up the aggregate--in fact, in this example the tetrachord is also a subset of the octachord--but they do belong to the complementary classes 4-12 and 8-12.
By the way, these examples demonstrate a valuable aspect of Forte's set-class names: classes and their complements are given the same ordinal numbers in his list. Classes 4-12 and 8-12 are complements, for example, as are classes 3-10 and 9-10, and classes 5-Z38 and 7-Z38. Because there are twelve pcs in the aggregate, trichords will be complements of nonachords, tetrachords of octachords, and pentachords of heptachords.
What about hexachords, which contain half the aggregate? They form a special case. "Non-Z" hexachord classes are always complements of themselves. For example, the complement of the whole-tone hexachord 6-35 [0,2,4,6,8,10] is another whole-tone hexachord 6-35, [1,3,5,7,9,11]. Z-related hexachord classes, however, are complements of their Z-mates. For example, the complement of hexachord 6-Z6 [1,2,3,6,7,8] is hexachord 6-Z38 [9,10,11,0,4,5].
Complementary sets can be an important feature of 12-tone music and of other music where the full chromatic aggregate is repeatedly used. While certainly more abstract, class complement relations can also be of value. For one thing, class complements sometimes seem to pop up in formally important junctures in atonal music. For another, there is a family resemblance between sets of complementary classes, based on similarities of their interval-class profiles. For example, the ic vector set class 4-12 is 112101; that of class 8-12 is 556543. Notice that in the octachord, there are four more copies of each interval class, except just two more of ic 6. All complementary sets are related in this way:
The difference in ic vector entries is equal to the difference in the sets' cardinalities (and to half that difference in the case of ic 6).
So ic vector entries will differ by 6 (3 for ic 6) between a trichord and its nonachord complement. They will differ by 4 (2) between tetrachord and octachord complements. They will differ by 2 (1) between pentachord and heptachord complements. And they will differ not at all between complementary hexachords--which is why hexachords form the "special case" outlined above.
It's also noteworthy that almost all sets larger than hexachords are capable of embedding their class complements as subsets. Composers may make use of such a combination of inclusion and complement relations. We may, for instance, find Stravinsky embedding sets of one of his favourite types, tetrachord 4-23 (0257) within passages based on the "diatonic octad" class 8-23 (0123578T).
Finally, you may find it useful, when calculating the prime forms of large sets, to deal with their complements instead. What, for instance, is the prime form of nonachord [7,8,9,10,0,1,2,3,4]? Well, the pcs it omits form set [5,6,11]. With a bit of experience, you can probably figure out in your head that the prime form of this trichord is (016) and that it belongs to class 3-5, so our nonachord must belong to class 9-5 (012346789).
| Exercise 14-1. Complement relations |
|
Key concepts on this page:
|
| Page last modified 10 July 2001 / GRT |
|
|||