|
|
|||
| 2. Intervals and interval classes |
Like the traditional pitch-class names, the traditional names of intervals are also biased by notions of tonal context; for instance, in tonal music, a minor 7th (say, C up to B-flat) and an augmented 6th (C up to A-sharp) are different intervals. Since such contexts are absent in non-tonal music, however, enharmonically paired intervals are also now equivalent: both a minor 7th and an augmented 6th are simply counted as an interval of 10 semitones. In all of our discussions of intervals, we shall use this system of semitone counts, again written with integers.
When we speak of intervals, we often use a few subtle levels of abstraction. In fact, we can think of four such levels, two when we measure the distance between pitches and two when we measure the distance between pitch classes.
Pitch intervals
Closest to our aural experience is the concept of ordered pitch intervals: we hear intervals of a particular size and direction between successive pitches. One pitch, for instance, might be 9 semitones above the previous one, or 15 semitones below. In Example 2-1, the ascending intervals between the pitches in Webern's melody are named with a "plus" (+) sign, descending intervals with a "minus" (-) sign.
Example 2-1. Webern, op. 3, no. 1, mm. 4-6. Pitch intervals

At times we may be concerned only with a pitch interval's size, not its direction. Then we speak of unordered pitch intervals. Removing the + and - signs from the interval names in Example 2-1 leaves only information about their size in semitones. Though this is a slight abstraction from our aural experience of melodic intervals, unordered pitch intervals are indeed a part of that experience when pitches are sounded harmonically. Then we hear intervals neither up nor down, just "between."
Pitch-class intervals
More important to our analysis will be two ways of thinking about the distance between pitch classes. We must understand a crucial difference between pitch classes and pitches: one pc isn't really "higher" or "lower" than another. Rather, the twelve pcs form a closed modulo 12 system, like the numbers on a clock face. We can think of measuring intervals between pcs like measuring clock time (see Example 2-2 below). What, for instance, is the interval between pc 4 and pc 11? There are two possibilities: "ascending" -- going clockwise -- it's 7 semitones; "descending" -- counterclockwise -- it's 5 semitones. Taking these two directions into account, we can measure pitch-class intervals.
Example 2-2. The pitch-class clock face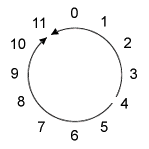
|
In measuring pc intervals we use modulo 12 arithmetic. The "ascending" clockwise interval from pc 4 to pc 11 is 7 semitones: 4 + 7 = 11. The "descending" counterclockwise interval is 5 semitones: 4 - 5 = 11. In modulo 12 arithmetic any addition or subtraction that goes past 12 or below 0 takes into account that 12 = 0 on the clock face. |
In Example 2-3 the intervals between the adjacent pcs represented by Webern's pitches are measured both "ascending" and "descending." Notice that the pairs of pc intervals are complementary: their integers always add up to 12.
Example 2-3. Webern, op. 3, no. 1, mm. 4-6. Pc intervals

We also use modulo 12 arithmetic to calculate intervals when we transpose pcs and groups of pcs. Though, as we've just seen, each calculation could be done in two directions, by convention pc transposition levels are calculated only in the "ascending" direction. In Example 2-4, the first five-note gesture of the Webern melody we've been considering is presented along with two other gestures, one that occurs earlier in the same song and one that occurs later.
Example 2-4. from Webern op. 3, no. 1. Pc transposition

The three gestures are clearly related: they are transpositions of each other. In terms of pc intervals, gesture a (pcs 1 5 4 7 2) may be transposed by 2 semitones (T2) to yield gesture b (pcs 3 7 6 9 4). In turn, gesture b may be transposed by 9 semitones (T9) to produce gesture c (pcs 0 4 3 6 1). We could easily work out the other transposition relationships among these sets, taking care to calculate clockwise.
| Exercise 2-1. Modulo 12 arithmetic and pc intervals |
Interval classes
In tonal theory, the axiom of octave equivalence underlies another familiar notion, that of interval "inversion". The perfect 4th and perfect 5th are said to be "inverses" of each other, as are the minor 3rd and major 6th, the major 2nd and minor 7th, and so on.
This is also true of their atonal counterparts: the complementary pc intervals of 7 and 5 semitones, of 3 and 9 semitones, of 2 and 10 semitones, etc. We shall use this relationship to propose that the pc intervals of each pair are equivalent, that they each belong to a single interval class (ic). In the following table, we can see how pc interval equivalence produces just seven interval classes, each named, by convention, for the smaller of its two pc intervals. (Ic 0 will not affect our analysis, so we'll be ignoring it).
| pc intervals: | 0 / 12 | 1 / 11 | 2 / 10 | 3 / 9 | 4 / 8 | 5 / 7 | 6 |
| interval classes: | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
The concept of interval classes is an abstraction that will prove useful when we begin to consider the properties of pc sets.
Summary
The table below summarizes the four levels at which we consider intervals. The example illustrates how the progressively more abstract concepts we apply have the effect of collapsing the distinct pitch interval types we hear into a small number of classes. Conversely, we can say that the few interval classes are each represented in actual music by several types of intervals. Ic 5, for instance, encompasses the eight ordered pitch intervals listed below, along with many more.
Example 2-5. Table of interval levels
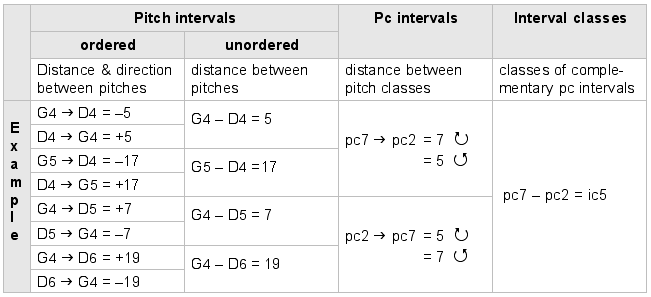
| Exercise 2-2. Pitch intervals and interval classes |
|
Key concepts on this page:
|
| Page last modified 17 July 2001 / GRT |
|
|||