|
|
|||
| 4. Pitch-class sets and normal form |
Pitch-class sets
Suppose we are analyzing Webern's "Dies ist ein Lied für dich allein," and we come upon the two segments presented in Example 4-1.
Example 4-1. from Webern op. 3, no. 1. a: m. 2, piano; b:
mm. 5-6 voice
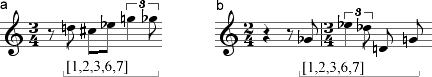
These two five-note segments share only one notated pitch, and they don't
project any clear tonal design. Might they nonetheless be related in pitch
structure?
If we apply the axioms of octave and enharmonic equivalence, we see that segments a and b are indeed related in a basic way: they comprise the same pitch classes: 2, 1, 3, 7, and 6. We can say, then, that these segments represent the same pitch-class set, and we can invent a set name for both segments that expresses their equivalent status. It could be any name, as long as it's the same one for both segments. We'll use a name that simply lists the set's pc content: "[1,2,3,6,7]." Labeling any future segments that have the same pc content "[1,2,3,6,7]" would express our perception that all such segments are equivalent according to our two basic axioms.
(By the way, we're used to segment equivalence in tonal analysis. Applying just the octave equivalence axiom, we routinely judge any segment that embodies pitch classes C, E, and G to be a "C-major triad." This includes the four different segments in Example 4-2, as well as countless others. The label "C-major triad" is a pc set name, isn't it?)
Example 4-2. Some C-major triads
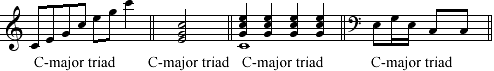
Naming sets: normal form
One of the abstractions of pc sets is that they are unordered, that is, the pcs may be embodied in any order in the musical segments. Segments in which pcs 1, 2, 3, 6, and 7 appear in the order 2, 1, 3, 7, 6 or 6, 3, 1, 2, 7 or 3, 1, 6, 1, 2, 3, 7, 2, or indeed simultaneously are all classified as belonging to the same set. Since we usually name a set by citing its pc content, it will help to have a standard order for listing the pcs; then all examples of the set will have the same name.
This standard order is called normal form. By convention, the normal form is the one that lists the pcs in ascending order and in the intervallically most compact form. Here are the steps for finding a set's normal form.
- Examining your segment, list its pc content, eliminating all pc repetitions.
- Arrange the pc integers in "ascending" (clockwise) orders.
Remember: these integers form a modulo 12 number group. Not only
can you "ascend" from 1 to 2, 2 to 3, 3 to 6, and 6 to 7;
you can also "ascend" from 7 to 1 (7 + 6 = 1). There are always
as many possible "ascending" orders as the set has pcs. For
pcs 1, 2, 3, 6, and 7, for example, the five orders are
1 2 3 6 7 2 3 6 7 1 3 6 7 1 2 6 7 1 2 3 7 1 2 3 6
- Now choose the most compact of the "ascending" orders: the
one whose interval span between the first and last pcs is smallest.
Do this by subtracting the first integer from the last.
Here the most compact "ascending" ordering is 1 2 3 6 7. This is the set's normal form, and the conventional name of the set will be [1,2,3,6,7]. The square brackets, commas, and lack of spaces between digits are also a convention in naming unordered sets (though some analysts use other conventions)."ascending"
ordersoverall span1 2 3 6 7 7 - 1 = 6 semitones 2 3 6 7 1 1 - 2 = 11 semitones 3 6 7 1 2 2 - 3 = 11 semitones 6 7 1 2 3 3 - 6 = 9 semitones 7 1 2 3 6 6 - 7 = 11 semitones
- The above steps are often enough to find a set's normal form. With
some sets, however two or more orders tie for overall compactness. The
rule then is to choose the set that is most compact towards the left.
Measure the intervals from first to second-last note. Still tied? Measure
from first to third-last note. Keep going until one set wins in compactness.
For example, name the set made up of pcs 1, 4, 7, 8, and 10.
As you can see, three of the five ascending orders are equally compact overall, spanning 9 semitones. Two of these still tie for compactness when we compare first to second-last pcs. Only when we compare first to third-last pcs does order 7 8 10 1 4 emerge as this set's normal form, the one most compact towards the left. We shall call this set [7,8,10,1,4]."ascending"
ordersoverall
spanspan
1st to 2nd-last pcspan
1st to 3rd-last pc1 4 7 8 10 10 - 1 = 9 8 - 1 = 7 4 7 8 10 1 1 - 4 = 9 10 - 4 = 6 8 - 4 = 4 7 8 10 1 4 4 - 7 = 9 1 - 7 = 6 10 - 7 = 3 8 10 1 4 7 7 - 8 = 11 10 1 4 7 8 8 - 10 = 10
- With sets of great intervallic regularity, no amount of interval measuring
will break the tie. Then choose the ordering that begins with the lowest
number. For example, name the set comprising pcs 2, 4, 8, and 10
Since interval measurement here doesn't produce a single most compact order, we simply choose [2,4,8,10] rather than [8,10,2,4] as the set's name."ascending"
ordersoverall
spanspan
1st to 2nd-last pcspan
1st to 3rd-last pc2 4 8 10 10 - 2 = 8 8 - 2 = 6 4 - 2 = 2 4 8 10 2 2 - 4= 10 8 10 2 4 4 - 8 = 8 2 - 8 = 6 10 - 8 = 2 10 2 4 8 8 - 10= 10
| Exercise 4-1. Naming sets using normal form |
|
Key concepts on this page:
|
| Page last modified 20 July 2001 / GRT |
|
|||