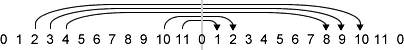|
|
|||
| 5. Pitch-class set classes and prime form |
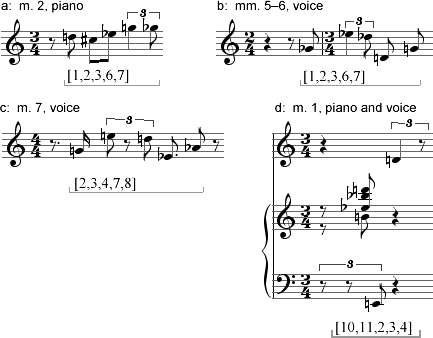
When our analysis uncovered musical segments a and b, cited again in Example 5-1 below, we found that these segments are related in a basic way: their pitch-class content is identical. We say they represent the same pc set, which we've named [1,2,3,6,7]. Suppose now that, in continuing to analyse Webern's song, we find two more segments, c and d, which we'll consider in turn.
Example 5-1. from Webern op. 3, no. 1
Axiom 3: Transpositional equivalence of sets
Now, even without pc set analysis, it's clear that segment c is quite similar to b: it repeats the same melodic gesture, just transposed. In pc set terms, however, c is considered to be related to both a and b: its pc set, named [2,3,4,7,8], is a transpositional equivalent of set [1,2,3,6,7]. If we were to take this new set and transpose each of its pcs by 11 semitones (T11), its pc content would be
2 3 4 7 8 + 11 11 11 11 11 = 1 2 3 6 7 set [1,2,3,6,7]
Theorists say that set [2,3,4,7,8] would "map onto" set [1,2,3,6,7] by operation T11. (And, of course, [1,2,3,6,7] maps onto [2,3,4,7,8] by operation T1.) Accepting an axiom of transpositional equivalence, we are going to to say that sets [2,3,4,7,8] and [1,2,3,6,7] belong to the same "type of set"; or, put another way, they are members of the same pc set class.
A moment's reflection will confirm that there are twelve pc sets like the two we've just met. Here they all are, listed in "ascending" order beginning on 0:
[0,1,2,5,6] [3,4,5,8,9] [6,7,8,11,0] [9,10,11,2,3] [1,2,3,6,7] [4,5,6,9,10] [7,8,9,0,1] [10,11,0,3,4] [2,3,4,7,8] [5,6,7,10,11] [8,9,10,1,2] [11,0,1,4,5]
They could all be mapped onto each other by transposition, so they are all sets of the same type -- all members of the same pc set class. We're going to need a label for this class, again to help us express our sense of set relatedness if we come upon more sets of this same class. Adopting one common convention, we'll call it class "(01256)". So, to sum up our analysis so far, segments a, b, and c in Example 5-1 embody two different sets, [1,2,3,6,7] and [2,3,4,7,8], but these two sets belong to the same set class, (01256).
(Again, by the way, we're used to transpositional set equivalence and pc set classes in tonal music. A C-major triad (containing pcs C, E, G) and an F#-major triad (F#, A#, C#) are transpositionally equivalent. They, and all the other major triads, are members of a pc set class whose class name is "major triad".)
|
|
Exercise 5-1. Set transposition and transpositional equivalence of sets |
Axiom 4: Inversional equivalence of sets
Finally, what about segment d in Example 5-1? Its pc content makes it an example of yet another set, [10,11,2,3,4], but one that cannot be mapped onto [1,2,3,6,7] or [2,3,4,7,8] by transposition (Notice that it's not in the list of 12 transpositionally equivalent sets above). It could be made to map, however, if we inverted it -- turned it upside down -- intervallically before transposing it (an operation called TnI).Let's see what would happen if we inverted this set. The common convention is to invert sets using 0 as an "axis of inversion" -- the central point around which the inversion takes place. To invert a set around 0, simply subtract each of its pcs from 0 (= 12). In such an inversion, pc 1 always maps to 11 (and vice versa), pc 10 to 2, pc 3 to 9, pc 4 to 8, pc 5 to 7 and both pcs 6 and 0 to themselves. So, set [10,11,2,3,4] inverts as follows:
Here's a graphical representation of the same inversion operation, in which the pcs are "flipped" around the 0 axis:
pc: 10 11 2 3 4 inverts to pc: 2 1 10 9 8
By doing this inversion, we have produced a new set, [8,9,10,1,2], and it happens that this is a set we could transpose to map onto the others (it is in the list above). Acording to a final axiom, Webern's set [10,11,2,3,4] is inversionally equivalent to sets [1,2,3,6,7] and [2,3,4,7,8]. Because of this, we shall classify it also as belonging to the same type of set -- as a member of set class (01256).
Of course, there are twelve sets that are transpositionally equivalent to [10,11,2,3,4] also. Here they are.
[0,1,4,5,6] [3,4,7,8,9] [6,7,10,11,0] [9,10,1,2,3] [1,2,5,6,7] [4,5,8,9,10] [7,8,11,0,1] [10,11,2,3,4] [2,3,6,7,8] [5,6,9,10,11] [8,9,0,1,2] [11,0,3,4,5]
These are all inversionally equivalent to all the 12 sets of our first list, so we now have a total of 24 sets that, through axioms of transpositional and inversional set equivalence, are considered to be members of the same set class: (01256).
|
|
Exercise 5-2. Set inversion and inversional equivalence of sets |
Briefly to recap: what is a pc set class? You can think of it as family of pc sets whose members -- according to axiom or convention -- are all related to each other by transposition (Tn) or by inversion (TnI). Some authors refer to pc set classes as "Tn / TnI types." If two sets can be mapped onto each other through one of these two operations they are classified as equivalent: they are held to belong to the same class. If not, they belong to different classes. Normally, a set class will have 24 member sets, as we've found class (01256) to have.
Naming set classes: prime form
As with naming sets, we need a conventional naming scheme for set classes, so that all sets we assign to the same class -- as we've done with [1,2,3,6,7], [2,3,4,7,8], and [10,11,2,3,4] for instance -- will be class-labeled identically. Since classes are defined by axioms of transpositional and inversional set equivalence, the conventional class name is one that reduces the (usually 24) normal form names of all the sets in the class to one supra-normal form called prime form. We cite the prime form of a set by putting it in a normal form, most compact towards the left, that begins on pc 0.
Here are the steps for finding the prime form of a set:
- Make sure your set is in normal form.
- Now invert this set, and place the result also in normal form.
- Now, transpose both normal forms to begin on 0.
- Finally, compare the two 0-transposed sets. Which is more compact towards the left? That one is taken as the prime form -- and the name of the class to which your original set belongs.
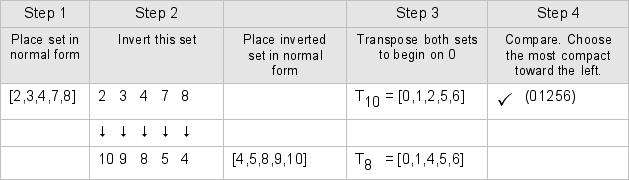
The tricky part can come in step 2. Normally if you invert a set, subtracting each of its integers from 0, the result will appear in "reverse-normal" order. You simply have to re-reverse this order to place your inversion in its own normal form. You can then proceed to steps 3 and 4. For example, here's the procedure for finding the prime form of set [2,3,4,7,8]:
However, the intervallic makeup of some classes of sets means that the normal form of a set and of its inversion are not always simply reverses of each other! For example, look what happens if we try to find the prime form of set [8,10,11,1,2,5]:
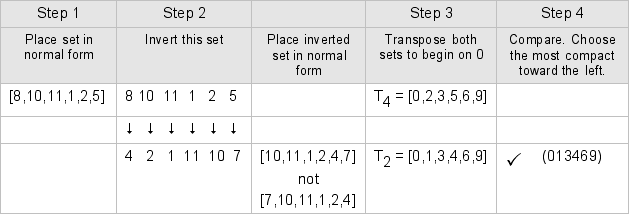
It turns out that the normal form of a set with pcs 4, 2, 1, 11, 10, and 7 is [10,11,1,2,4,7] -- something you should be able to verify for yourself by now. In this case, if you were to carry out Step 2 carelessly, merely reversing the digits of your inversion, the normal form -- and then the prime form -- you end up with would be incorrect! Since you can never tell when you'll face a set of this sort, you must always take care when normalizing sets.
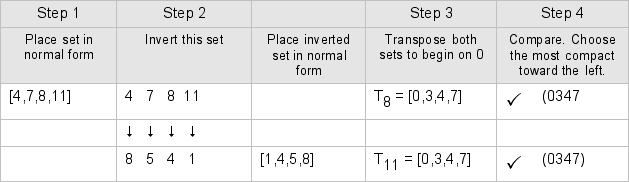
Finally, some sets are inversionally symmetrical. As the example below shows, making your final choice of prime form is easy here: the original set, and its inversion produce the same result when transposed to 0. Let's try set [4,7,8,11].
| Exercise 5-3. Classifying sets using prime form |
|
Key concepts on this page:
|
| Page last modified 24 July 2001 / GRT |
|
|||